Exercise 1

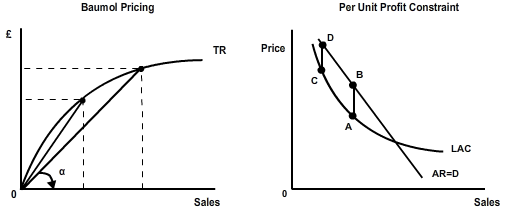
A market share model generally addresses the issue of market price. We argued in Study Guide Unit 1 that the Baumol firm will have a lower price than the profit maximising firm. Figure 1 accompanying this section illustrates this point by an application of the derivation of price using an angle measure as illustrated in Figure 1.

A per unit profit constraint also manifests itself across the pricing practices of a modern firm. Figure 2 illustrates the per unit profit as the vertical distance [AB], the difference between per unit average cost at point A and price at point B. Notice that as price increases that the per unit profit, the vertical distance [AB] decreases to [CD]. Hence as price increases per unit profit decreases, that is, δ[AB]⁄δP < 0. In other words, there is an upper limit to the level of market price that a firm can exact on the consumer. This is the per unit profit constraint; the constraint is internal to the firm in that management soon realise that a successively higher price does not translate into higher per unit profits. A discussion of this issue will feature in Unit 3’s review on elasticity. At this juncture, suffice to note that regardless of the behaviour of management, there is an upper limit to the level of market price.

Exercise 2

Is it possible that the Baumol firm will reach the point of maximized before the profit constraint is satisfied? The answer is no if two conditions hold:

• if advertising expenditures are variable,
• if the Baumol assumption that the of additional advertising is positive.

When these occur excess profits will be spent on advertising and the schedule will shift upwards until the profit constraint is satisfied. And the schedule is still increasing.

Recall that the difference between a static and a dynamic Baumol firm in that profits are reinvested by a dynamic firm for further growth.

Exercise 3

Examine the impact on the short run equilibrium position of the firm of an increase in total fixed costs.

The objective here is to examine the impact on both short run price and output of an increase in total fixed costs [TFC]. The traditional theory of the firm suggests that an increase in TFC has no impact on the equilibrium of a profit maximizing firm. As the firm’s profit is reduced neither the output nor the price change. For a Baumol firm however this is not the case. As illustrated in Figure 1(a) an increase in TFC reduces the short run level of output to q2 from q1. For the Baumol firm an increase in TFC also reduces profit. This can be illustrated by shift downwards in profit function. If the profit constraint was binding before the increase in TFC, it will no longer be met after the increase; the level of output will have to be reduced before the profit constraint can again be satisfied. The reduced output will be sold at a higher price.

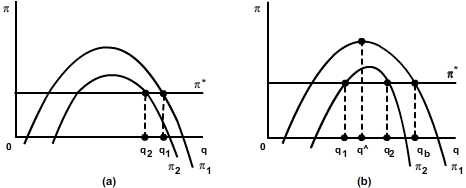
When variable costs increase as illustrated in Figure 1(b) both firms reduce output. However, the reduction in output is less for the profit maximizing firm as constructed |q^–q1|<|qb–q2|. One could convert the change in output into an elasticity measure defined as Δq⁄ΔTVC; the smaller the value of the elasticity coefficient the more likely it is that the firm is a profit maximizing firm. Since other managerial theories of the firm predict that a firm will react to an increase in costs by reducing output, the observation that firms do behave like this is not conclusive proof that they are Baumol firms. It would be necessary to determine the MC = MR level of output [say] = q^; since the Baumol firm’s level of output qb is greater than any other firm’s output q then one could argue that |qb–q^|>|q^–q| would represent a necessary condition. If the necessary condition holds then Δqb⁄ΔTVC>Δq⁄ΔTVC should hold in general.

Exercise 4

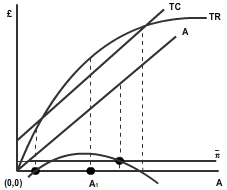
Construct the diagram for the Baumol static single-product model with advertising.

Figure 1 supplies the answer. With advertising, it is not possible to have an equilibrium where the profit constraint is not operative. Increased advertising will increase sales revenue, hence the sales maximizer will increase advertising expenditure to level A1 until prevented from doing so by the profit constraint.