The Bertrand-Edgeworth Model

The Bertrand-Edgeworth model examines the pricing behaviour of interdependent firms in a product market with few rival firms. With two rival firms, the product market is defined as a duopoly, with more than three but less than seven the product market is defined as an oligopoly. Bertrand replaced price as the variable in Cournot’s original assumption on zero conjectural variation. The essence of the Bertrand model as illustrated in Figures 1 and 2 is that oligopolistic firms shade price in order to monopolise the market. We advance price shading into a fooling-the-rival behavioural strategy in the next section. Edgeworth modified the Bertrand model in assuming that rival firms cannot completely supply the entire market. This limitation on output supply precludes the attainment of the Bertrand zero-price solution as illustrated in Figure 4 at (0,0). The modification is made to the original Bertrand model by allowing the reaction functions to intersect with the axes.

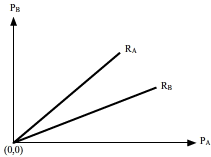
• the possibility of non-intersection of the reaction curves which assumes zero costs of production, and
• the intersection of the reaction curves respectively.

The latter represents the Edgeworth modification of the Bertrand model. Both models indicate a market structure beset by recurrent price instability. In support of the Sweezy model earlier, we have a reason for the alleged inflexibility in oligopolistic markets in the apparent unwillingness of management in one firm to unilaterally change price. The principle behind the reaction functions is that they allow each representative firm to react to the price changes of a rival firm within the parameters set by an equal or no-change in the representative firm’s profits.

Fooling-The-Rival Behaviour and Price Looping

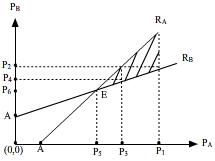
Here we look briefly at the fooling behaviour of modern management engaged in episodic price wars. The episodic price war is represented by the shaded area in Figure 3. Firm A begins with p1 and firm B retaliates with p2 to which firm A responds with p3. Firm B responds further with p4 and the sequence of price movements converge to an equlibrium market-at-rest at E with firm A charging p5 and firm B charging p6. It is important to note that p5≠p6. This fooling behaviour is an interesting aspect of modern management behaviour and may offer some gem of wisdom in understanding the complexities of the competitive process. Episodic price wars are ubiquitous from transatlantic airfare wars to PC price reductions worldwide to localised price wars over the price of bread.

The management of the firm concerned may opt to create a pattern of price movements which are erratic yet the rivals so recognise this price movement as characteristic of the firm. The representative firm exploits the belief structure of the rival firms. In other words, the rival firms are able to chart the price moves in a sequence of loops. Firstly, the representative firm increases price, denoted by ↑ and of course rival firms do not react; then suddenly the firm reduces price to below the original price, denoted by ↓, and this immediately forces the rivals to counteract by reducing their prices. Once this has occured the original firm reduces price again and as before so do the rival firms. The price reductions end here in order to avoid a price war. At this stage rival firms expect the first firm’s price incease to be followed by an instant price reduction, therefore they observe as characteristic of this firm, a set of price moves defined by the price loop ψp = ↑↓↓.

Realising this, management now decides its ultimate plan in fooling the rival firms - the objective may be to capture sales through price reductions by sufficiently fooling rivals on price. After a couple of weeks or months have elapsed with price looping, management reduces price to p^ below the original p* level and rival firms do likewise. Then the firm immediately responds by raising price back to the original level and the rival firms, expecting a price reduction based on past experience, remain at the p^ level regarding this price as the minimum price level of the firm. They are content to remain at p^ as they are undercutting the representative firm. They also believe that since the representative firm has a higher relative price, the price loop ψp sequence will imply an eventual reduction in price.

Perceived Reaction Function

The rival firms adjust to this anticipated [price loop induced] reduced price level; depending on the elasticity of the demand relationship the representative firm remains at the higher price level. Then it drastically cuts prices to below the p^ level. We assume that the rival firms are slow to react because they are suspicious of the management’s intentions and while they consider their countermove, the firm with the product on offer at the reduced price, has increased sales at the margin. On identifying this fooling behaviour, the rival firms similarly reduce price; in the long run the representative firm establises itself as the price leader in this product-market. Management have induced a sequence of price moves which may allow their representative firm to overcome the inelastic nature of the demand relationship in the lower price ranges. The original price p* as illustrated in Figure 1 acts as a pivot as the inelastic [DE] segment shifts out to the become more elastic. After a period of time the representative firm consolidates market share and a new higher kink price is established.

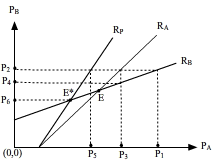
The price-looping fooling behaviour can be mapped into the reaction functions where RP is the perceived reaction function as illustrated in Figure 4. Let firm A, the fooling firm, initiate the price changes with p1 to which firm B replies with p2. The choice of p2 was contingent on some knowledge of A’s reaction function, that is, in believing that firm A will respond with p3 to which B further responds with p4; but in the interim, firm A has fooled B and responded to p2 with p5 on the RP reaction function such that p5 < p4. Now at p5 firm B would not respond as the price combination is below the equilibrium level E. Firm B was fooled into believing that p1 was to lead to p3 when in fact firm A’s initial intentions were to reduce price to p5. Alternatively firm B’s management could respond with p6 a “call the bluff of firm A” strategy, which would reduce the market price to E* level which is less than p5, the price firm A had competed for in the market. How best do the management of firm B respond? Which reaction function do they monitor? If firm B regarded RA as the appropriate reaction function, it remains at p4, otherwise the RP function dictates a continuation of the price war to E* with p6 as a final market-at-rest price. The unequal market shares contingent on this final price will engage the firms in contest competition and the market eventually collapses into a market system.